Linux-Projekte für den Raspberry Pi
(in Python realisiert)
[Hardcopy vom monochromen LCD-Inhalt erstellen (.gif)]



Nachdem mehr und mehr Daten auf dem LCD-Display angezeigt werden konnten, wurde es zunehmend interessanter, diese Anzeigen auch zu archivieren oder auszudrucken. Daher wurde dieses Projekt ins Leben gerufen.

Da es sich in diesem Beitrag hauptsächlich um Theorie handelt wird es jetzt leider ziemlich 'trocken':

Zunächst wurden die Rasterdaten des LCD, die ja im programminternen Pufferspeicher vorlagen, als BMP-Datei angespeichert. Dies ließ sich relativ einfach verwirklichen. Da es sich aber um ein unkomprimiertes Verfahren handelt, nahmen die erzeugten Dateien in Summe nach und nach beträchtlichen Speicherplatz in Anspruch. Also wurde nach einem relativ einfachen Ausweg gesucht. PNG und PDF kamen wegen der Komplexität der Dateien nicht in Frage.
Schlußendlich wurde die GIF-Kodierung gewählt. Diese schien mit dem geringsten Aufwand realisierbar..

Dazu mußten die LCD Daten zunächst aus dem programminternen Pufferspeicher des LCD-Displays in serielle Rasterdaten umgewandelt werden. Dies ließ sich relativ schnell verwirklichen. Danach gingen die Probleme aber schon los.

GIF verarbeitet die seriellen Daten nicht Byte oder Wortweise, sondern in variabler Bitanzahl. D.h. die Länge der jeweils zu verarbeitenden Daten variiert von 2 bis 12 Bit. Damit war klar, es mußte wieder ein interner Pufferspeicher (GIF-Speicher) erzeugt werden.


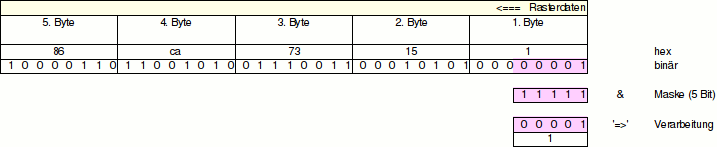
Als Beispiel für die Bitaufteilung eine Grafik mit 5 Bit

Die Eingangsbytes der Rasterdaten werden, im Prinzip, alle aneinandergehängt.
Ab dem 1. Bit wird dann eine 'Maske' mit der notwendigen Bitlänge 'darübergelegt'

Hier der erste Schritt (mit5 Bit als Beispiel)
Das 1. Byte der Rasterdaten (01) wird durch

UND mit der Maske (1F) verknüpft.

Ergebnis ist die Zahl 1

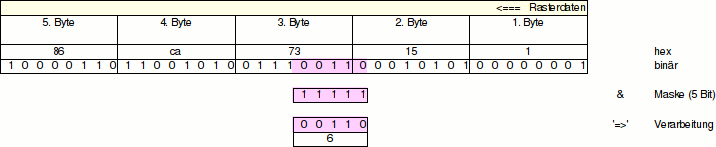
Jetzt wird die Maske um die Anzahl der erforderlichen Bits (5) nach links verschoben
Damit wird nun Byte 1 und 2 der Rasterdaten behandelt (15,01)

UND mit der Maske (1F) verknüpft

Ergebnis istdie Zahl 8

Wieder wird die Maske um die Anzahl der erforderlichen Bits (5) nach links verschoben Byte 2 der Rasterdaten (15) wird mit

UND mit der Maske (1F) verknüpft

Ergebnis ist die Zahl 5

Erneut wird die Maske um die Anzahl der erforderlichen Bits (5) nach links verschoben Byte 2 und 3 der Rasterdaten (15, 73) wird mit

UND mit der Maske (1F) verknüpft

Ergebnis ist die Zahl 6


So geht das weiter, bis alle Rasterdaten abgearbeitet sind.
Das heißt, im laufe der Codierung (Weiterverarbeitung) der so erzeugten Daten ist es notwendig, die Bitanzahl der 'Maske' zu variieren. Daher muß die Maske und deren Verschiebung variabel gestaltet werden.
Das Beispiel hier zeigt nur die reine Theorie. Wie das genauer geht habe ich in diesem Fall versucht darzustellen.

Die Ergebnisse dieser Aufteilung sind die Eingangsdaten für die danach folgende LZW-Codierung


  • Zu Beginn der Codierung werden verschiedene Bedingungen gesetzt:

    • der Bitanzahl-Zähler wird initiiert (4 Bit – meist werden hier 8 Bit gesetzt. Ist einfacher!)
      (Die Bitanzahl 4 wurde von mir zu Testzwecken gewählt und nie verändert)

    • Die BitMaske wird auf die Anzahl der Bits gesetzt (0x0F / 0b1111 = 4 bit)

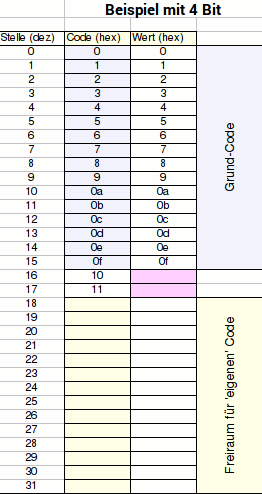
    • eine Codetabelle wird initiiert

  • diese besteht aus einem Dictionary mit Key == Wert
    In diesem Beispiel ist der 'KEY' als Code dargestellt und der 'Wert' eben als Wert.

    Mit 4 Bit kann bis (2^ 4) 16 gezählt werden. Also wird eine Tabelle mit 16 möglichen Einträgen erstellt.
    FALSCH gedacht!
    (DAS herauszufinden hat mich wirklich VIELE graue Haare gekostet)

    Ja, es wird eine Tabelle gebildet,
    aber mit 2^ (Bitanzahl PLUS Eins) Einträgen (also 0-31)

    Diese Tabelle wird bis 2^ Bitanzahl (0-15) mit der eigenen Stellen-Nummer gefüllt. Es erhalten somit 'Key' und 'Wert' den gleiche Wert.

  • Es folgen noch 2 Sonderfälle:
    2^ (Bitanzahl). Bei 4 Bit ist das 16, den Clear Code („CC“) und
    2^(Bitanzahl) +1. Bei 4 Bit ist das 17, den End of File Code („EOF“).

    Diese haben im Verlauf der Codierung eine besondere Bedeutung.

    Der 'Rest' der Tabelle [2^(Bitanzahl)+2 bis 2^(Bitanzahl+1)-1]
    (18 – 31) steht für eigene Codes zur Verfügung
    (Im Endeffekt stehen also nur 2^(Bitanzahl) -2 Stellen für die Codierung zur Verfügung)


      • Der ClearCode 'CC' wird als allererster Wert in den Ausgabestrom geschrieben

      • Der FreiCode Zähler wird initiiert. Bei 4 Bit= 18 (der 1. Wert nach EOF. An dieser Stelle wird der 'eigene' Code angespeichert).


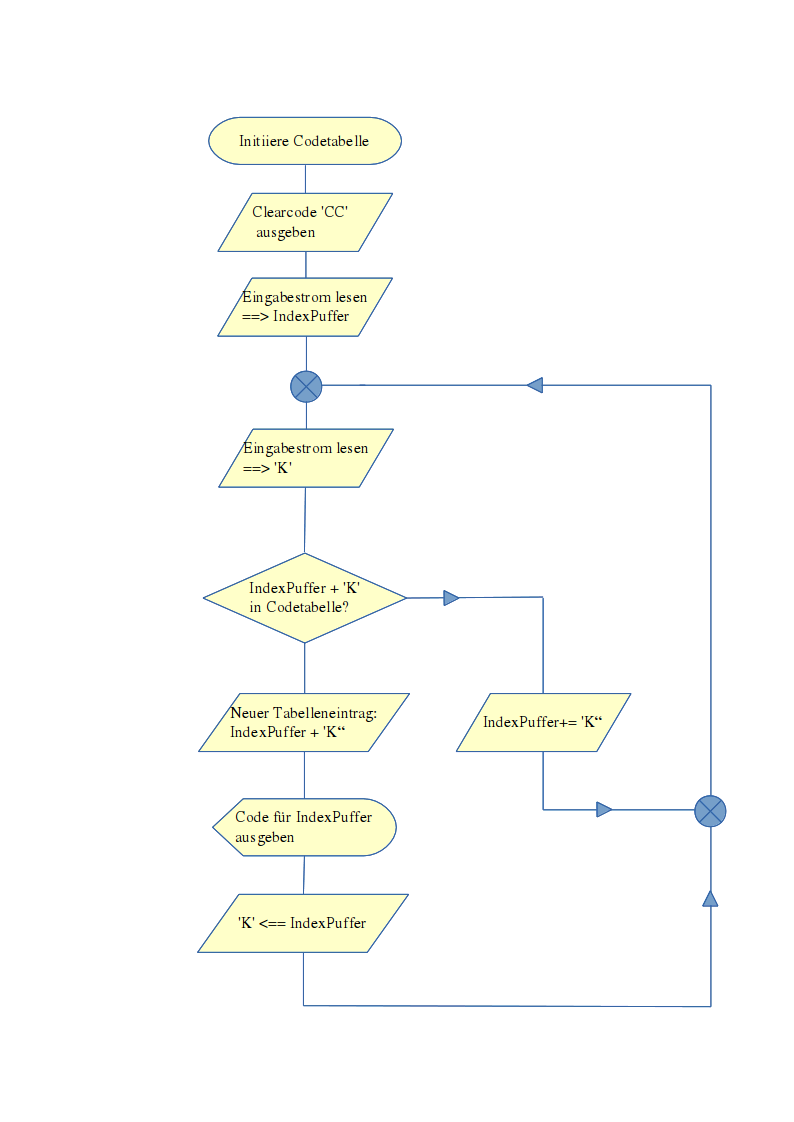
Hier nun exemplarisch die Codierung



Codetabelle initiieren (siehe Oben)


ClearCode 'CC' ausgeben (siehe Oben)

Wert in Variable 'Altwert' einlesen


Schleifenbeginn

Nächsten Wert in Variable 'Neuwert' einlesen


'Altwert' + 'Neuwert' in Codetabelle enthalten?
JA:

An Variable 'Altwert' Variable 'Neuwert' anhängen



NEIN:

Neuen Tabelleneintrag mit 'Altwert' + 'Neuwert' erzeugen
Code für 'Altwert' ausgeben
Variable 'Altwert' mit 'Neuwert' überschreiben


Wenn weitere Daten im Eingabestrom:
zurück zu Schleifenbeginn


sonst: Code für 'Altwert' ausgeben

'EOF' Code ausgeben

Mit den ausgegebenen Daten weiter zum 'Packen'


        Wird der letzte freie Wert in der 'CodeTabelle' belegt, muß die 'Tabelle' gelöscht und mit einem Bit mehr neu aufgebaut werden:
        Das hieße dann

        • bei bisher 4 Bit nun 5 Bit

        • Codetabelle von 0x0, 0x1... 0x1F, 020 (CC), 021(EOF)

        • 1. Freicode 0x22

        • letzter möglicher Eintrag (0x2F)

        • Bitanzahl_neu: 5

        • Bitmaske_neu: 0x02F …......

  • Ist die Länge der Daten im GIF-Speicher NICHT ausreichend für die aktuelle Verarbeitung (Bitanzahl) , wird ein Byte (8 Bit) aus den Rasterdaten geholt, um die noch vorhandene Bitanzahl im Pufferspeicher nach links verschoben und über ODER (|) in den aktuellen Gif-Speicher eingefügt (das heißt einfach, die neuen 8 Bit werden - von links her - an die alten Daten angefügt).

  • Stehen genügend Bit für die Verarbeitung bereit, startet die Kodierung.

  • Aus dem GIF-Speicher werden über die zu Beginn gesetzte Maske mittels UND Funktion die notwendigen Bits vom Anfang her herausgefiltert (IstWert).

  • Anschließend werden die verarbeiteten Bits aus dem GIF-Speicher gelöscht. (um die Bitanzahl nach rechts verschoben, also rechts weggenommen )
    Ein Beispiel dazu ist ___HIER___


Eine Besonderheiten gibt es natürlich trotzdem noch:

    • Ist die Bitanzahl > 12,

      • wird die gesamte Initiierungsprozedur nochmals duchgeführt (Codetabelle neu aufbauen, Bitzähler auf 4 setzen......)

      • muß ein CC = ClearCode in die Zwischendatei geschrieben werden, damit später der Dekoder weiß, er muß mit der Bitanzahl 4 neu anfangen
        Ein CodeTabelle kann also nie mehr als 4kB Einträge enthalten.

  • Nun geht es wieder von Vorne los, bis das Ende der Rasterdaten erreicht ist


Eigentlich ist die ganze CODIERUNG doch recht simpel. Aber das Drumherum macht das Verständnis dann doch etwas schwierig ;-).